Chaque vendredi, je publie sur ce blogue de petites énigmes logico-mathématiques, ainsi que la solution des énigmes de la semaine précédente.
Merci de ne pas poster vos solutions ici, afin de permettre à tout le monde de jouer.
Les questions demandant des éclaircissements ou des précisions sont par contre les bienvenues.
Enigmes de la semaine
1. L’image suivante, faite avec des allumettes, représente un verre contenant une olive. Il s’agit de redessiner ce verre, mais sans son olive (qui sera donc à l’extérieur du verre) et en ne déplaçant que deux allumettes. Le verre, à la fin de l’opération, peut se retrouver dans n’importe quelle position.
2. Voici un poisson. En ne déplaçant que trois allumettes, faites-le nager dans la direction opposée.
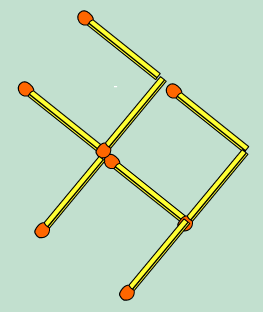
3. Voici un arrangement de cinq carrés identiques. En ne déplaçant que deux allumettes, vous devez ne laisser que quatre carrés identiques.

Solutions aux énigmes de la semaine dernière
1. En prenant deux personnes quelconques dans un ensemble de six, elles doivent forcément s’aimer ou se haïr et il n’y a aucun groupe de trois personnes qui s’aiment mutuellement. Le problème consiste à démontrer qu’il doit exister un groupe de trois personnes qui se haïssent mutuellement.
Il est facile de le résoudre par la méthode des graphes. Six points représentent les six personnes (voir la figure ci-après). Tous les couples possibles sont joints par un trait pointillé symbolisant une relation d’amour ou de haine. On admettra que l’amour est représenté par des lignes bleues et la haine par des lignes rouges.
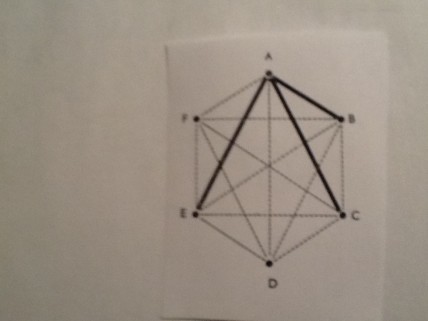
Considérons la personne A. Sur les cinq segments qui rayonnent à partir d’elle, trois au moins doivent être de même couleur. Le raisonnement reste valable quelle que soit cette couleur et quelles que soient les trois lignes; nous supposerons donc que trois segments sont rouges (ceux qui sont en traits forts sur la figure). Si les segments qui forment le triangle BCE sont tous bleus, nous avons un ensemble de trois personnes qui s’aiment mutuellement. Mais l’énoncé nous précise qu’un trio de ce genre ne doit pas exister; l’un des côtés du triangle, au moins, doit donc être rouge. Quel que soit le côté que nous considérons comme rouge, nous sommes certains de former un triangle entièrement rouge, c’est-à-dire un trio lié par une haine mutuelle. Nous aurions obtenu le même résultat si nous avions admis que les trois lignes étaient bleues au lieu de rouges. Dans ce cas, les côtés du triangle BCE auraient tous été rouges puisqu’un seul côté bleu aurait permis la création d’un triangle entièrement bleu. En résumé, il doit donc y avoir au moins un triangle entièrement bleu ou entièrement rouge. L’énoncé éliminant la possibilité d’un triangle entièrement bleu, il ne reste que celui qui est entièrement rouge.
On peut d’ailleurs aller plus loin. S’il n’y a aucun triangle entièrement bleu, on peut démontrer (par un raisonnement un peu plus complexe), qu’il doit y voir au moins deux triangles entièrement rouges. Dans la théorie des graphes, tout graphe chromatique de ce genre qui n’a aucun triangle bleu est dit graphe chromatique vide en bleu. Si le nombre de noeuds est égal à six, comme dans notre problème, le nombre minimal de triangles rouges est égal à deux.
Quand le nombre de noeuds d’un graphe vide en bleu est inférieur à six, il est facile de le tracer sans triangle rouge. Si le nombre de noeuds est égal à sept, il doit y avoir au moins quatre triangles rouges. Pour un graphe vide en bleu à huit noeuds, le nombre minimal de triangles rouges est égal à huit; il passe à treize quand il y a neuf noeuds. (Martin Gardner, Le paradoxe du pendu et autres divertissements mathématiques, pp. 175-176)
2. […] La solution la plus courte a été trouvée par Goran Ohlin, un économiste de l’université de Columbia.
Celle qui a servi la première a servi cinq fois de suite et l’autre a servi quatre fois. Supposons que celle qui avait le premier service ait remporté x de ses cinq balles et y des quatre autres balles. Le nombre total de balles perdues par les joueuses sur leur service est donc 5 — x + y. Ce nombre est égal à 5 puisque l’énoncé précise que cinq balles ont été gagnées par la joueuse qui avait le service; il en résulte que x = y et la première adversaire a donc remporté 2 x balles en tout. Comme Miranda seule a gagné un nombre pair de balles, elle a forcément été la première à servir. (Idem, p. 79)
3. Pour trouver la distance parcourue par les Smith au cours de leur voyage du Connecticut en Pennsylvanie, les heures de la journée qui fuguent dans l’énoncé ne servent à rien puisque Smith conduit à une vitesse variable. En deux points de la route, Madame pose une question. Les réponses de monsieur indiquent respectivement que la distance du premier point au restaurant de Patricia Murphy est les deux tiers de celle du point de départ au même restaurant et que la distance du restaurant au second point est les deux tiers de celle du restaurant à la fin du voyage. Il est donc évident que la distance qui sépare ces deux points, et nous savons qu’elle est égale à 200 miles, représente les deux tiers de la distance totale. Cette dernière est donc égale à 300 miles. ( Idem, p. )

