Du 14 au 22 mars, c’est la Semaine des mathématiques.
Celle de 2015 marque aussi le 101e anniversaire de naissance de Martin Gardner (1914-2010), un homme qui a, avec raison, été décrit comme le meilleur ami que les mathématiques ont eu le bonheur d’avoir.
Gardner est un de mes héros. Avec Prévert, Chomsky et Russell, il est un des rares auteurs dont je collectionne les écrits, moi qui ai toute ma vie passionnément acheté des livres. Mon Petit cours d’autodéfense intellectuelle lui est dédié et je garde précieusement la lettre qu’il m’a écrite quand je le lui ai envoyé.
Immense Gardner
Formé en philosophie, Gardner est un polymathe, un touche-à-tout qui a non seulement brillamment et abondamment écrit en philosophie, mais aussi sur la littérature, sur les sciences (naturelles et sociales), sur la magie (qu’il pratiquait) et sur la religion. Il a également fondé le mouvement sceptique contemporain.
Et ce n’est pas tout. Ayant créé et tenu durant plus de 25 ans la légendaire chronique «Jeux mathématiques» de la revue Scientific American, Gardner est probablement la personne qui, au 20e siècle, aura le plus fait pour rendre populaires les mathématiques. Bref, P. W. Diaconis avait entièrement raison quand il lançait son malicieux avertissement: «Mise en garde: Martin Gardner a transformé des douzaines d’innocentes jeunes personnes en professeurs de mathématiques et des milliers de professeurs de mathématiques en innocentes jeunes personnes.»
Je vous laisse découvrir son imposante et diversifiée bibliographie (plus de 100 titres) et vous propose cette fois de vous parler de Gardner le didacticien des maths: il y a là tout un territoire qui reste largement inexploré et dont on tirerait, il me semble, un beau sujet de mémoire.
Tic-tac-toe et autres mathématiques récréatives
Gardner a souvent raconté comment enfant, en classe de mathématiques au primaire, ayant complété le travail demandé, il s’amusa à chercher la réponse à la question suivante: si chaque joueur d’une partie de tic-tac-toe joue chaque fois son meilleur coup, est-ce le premier à jouer qui l’emporte, le deuxième ou font-ils match nul?
L’apercevant en train de griffonner, son enseignante déchira sa feuille de travail en lui expliquant que dans sa classe de maths, on ne devait faire que cela: des maths.
Gardner était, et restera, incapable de lui donner raison.
Ce qu’il faisait ce jour-là, soutient-il, c’était non seulement des maths, mais c’était aussi des mathématiques rencontrées sur un terrain qui permet à la fois de les connaître et de les aimer. D’où cette passion qu’il aura sa vie durant pour les jeux, les énigmes, les curiosités, les illusions cognitives et toutes ces autres manières ludiques de faire connaître des idées et des concepts mathématiques.
Voici trois exemples de ces mathématiques récréatives qu’on pourrait utiliser en classe.
ABCABC
Demandez à vos élèves de choisir un nombre composé de trois chiffres: ABC, disons 237. Demandez-leur ensuite d’entrer ce nombre deux fois dans une calculatrice, ABCABC, ici: 237237.
Dites-leur ensuite que vous avez le pouvoir de prédire que s’ils divisent le nombre choisi par 13, il n’y aura pas de reste. Ensuite, s’ils divisent le résultat obtenu par 11, il n’y aura pas de reste non plus. Et finalement, s’ils divisent ce dernier résultat par 7? Bingo! Revoici ABC.
L’explication? ABCABC = ABC x 1001 = ABC x 7 x 11 x 13. Et 1001, comme tout entier naturel, peut être décomposé en un ensemble unique de nombres premiers.
Je vous laisse décider ce qu’on peut faire avec cela pour initier vos élèves à la théorie des nombres et aux nombres premiers, selon le niveau considéré.
Mathémagie algébrique
Allons à présent en classe d’initiation à l’algèbre, où nous croisons une magicienne — ou plutôt une mathémagicienne.
Elle demande à un volontaire:
«Pensez à un nombre, n’importe lequel, mais sans me le dire.
Ajoutez-lui 15.
Multipliez le résultat par 3.
Soustrayez 9 à ce résultat.
Divisez le résultat obtenu par 3.
Soustrayez 8.
Dites-moi à quel résultat vous arrivez.»
Et la mathémagicienne annonce alors le nombre qu’avait choisi la personne volontaire!
Le truc marche à tout coup, et comprendre pourquoi et comment est un bel exercice d’initiation à l’algèbre.
Disons que le nombre de départ est n.
On a fait: n + 15. Puis: 3 (n + 15), soit 3n + 45. Puis: 3n + 45 – 9, qui nous donne comme résultat: 3n – 36. En divisant ce résultat par 3, on obtient: n + 12. On a ensuite soustrait 8 de ce résultat, soit: n + 12 – 8, ce qui nous donne: n + 4.
Le résultat auquel arrive le volontaire est donc toujours le nombre qu’il avait choisi au départ, plus 4. La mathémagicienne, pour retrouver le nombre choisi au départ, n’a donc qu’à soustraire 4 du résultat annoncé.
64=65 ?!?
Allons à présent faire un tour en classe de géométrie.
Considérez ces deux figures.
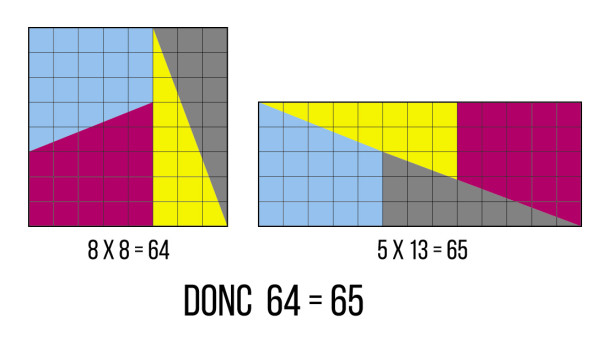
Comme on peut le constater, celle de droite a une surface de 64 unités et celle de gauche, de 65 unités. Pourtant, elles semblent composées des mêmes figures géométriques, qui sont simplement organisées différemment chaque fois. Les élèves peuvent d’ailleurs s’amuser à reproduire la première figure et à en manipuler les composantes pour obtenir la deuxième.
Voici des questions qu’ils et elles se poseront — et avec un peu d’aide, résoudront.
A-t-on réellement prouvé que 64=65?
Si non, pourquoi?
Et si c’est une illusion, comment fonctionne-t-elle?
Avant de demander l’aide de madame Google, tentez de résoudre par vous-même cette énigme à l’aide des découpages.
Amusez-vous bien!
Si vous ne trouvez pas la solution, visitez: http://therese.eveilleau.pagesperso-orange.fr/pages/paradoxe/textes/fibo2.htm.
Allez-y: vous n’en reviendrez pas!

3n + 36, évidemment. Désolé.
C’est un vieux truc qui ne semble marcher qu’à cause des différences minimes qu’il y a entre les pièces qui composent la construction. La surface manquante est distribuée de part et d’autre tout au long de l’arête de la diagonale du rectangle « construit ».
Pour s’en convaincre, on peut faire appel au bon vieux théorème de Pythagore: c^2 = a^2 + b^2
La diagonale du rectangle « théorique » correspond à la longueur de l’hypothénuse du triangle (figure de droite) devrait être (5^2 + 13^2)^1/2 = (25 + 169)^1/2 = (194)^1/2 = 13,9283882772
La longueur de la diagonale obtenue par construction est égale à la longueur de l’hypothénuse du triangle de côtés 8 par 3 plus la longueur de l’hypothénuse du triangle de côtés 5 par 2 (qui correspond au côté du trapèze).
La diagonale du rectangle «construit» = (8^2 + 3^2)^1/2 + (5^2 + 2^2)^1/2 = 73^1/2 + 29^1/2 = 8,5440037453 + 5,3851648071 = 13,9291685525
Donc la diagonale de la figure obtenue par construction est un peu plus grande. Comment est-ce possible? En fait, ce n’est pas la « vraie diagonale » de pente 5 / 13 = 38, mais une ligne brisée qui se se compose de deux parties de pentes légèrement différentes 3/8 = 0,375 et 2/5 = 0,4. La différence de surface est un losange manquant qui complète la figure.
J’ai trouvé une figure tres explicite sur Internet: http://mathematicscentre.com/taskcentre/images/155c6465.gif
—–
En passant, mon Martin Gardner à moi s’appelle Pierre Berloquin. Pierre vit en France entre Paris et Bossay-sur-Claise et il a tenu pendant plusieurs années la chronique mathématiques de la revue Science&Vie et il a écrit de nombreux livres d’énigmes et de jeux mathématiques. Pierre qui se définit comme un « ludologue » est devenu mon ami par le hasard des rencontres d’un monde vraiment très petit… ou d’un Petit monde…
Oups! de pente 5 / 13 = 0.38
Sincèrement, je trouve que les exemples donnés ne sont pas les meilleurs exemples d’utilisation des mathématiques ludiques pour l’apprentissage.
Le problème, c’est que ces exemples n’apportent pas de plus-value réellement appréciable comparé à d’autres exemples non-ludiques : bien souvent, les problèmes de mathématiques ludiques donnés n’apprennent que des connaissances beaucoup trop spécifiques, non-transférables, qui ne peuvent pas s’appliquer à de nombreuses situations.
Pour le premier exemple que vous donnez dans votre billet de blog, tout ce que l’élève apprend, c’est que 1001 = 11 * 13 * 7. C’est un peu la même chose avec le troisième exemple : beaucoup de vernis sur pas grand chose. Alors certes, c’est amusant, mais niveau apprentissage, c’est très faible.
A la rigueur, le second exemple peut parfaitement servir d’exercices pour apprendre à l’élève de modéliser un problème sous forme algébrique pour des élèves qui ont un peu de bouteille. Il faut bien le reconnaitre que celui-ci sort un peu du lot.
Mais hormis quelques rares exception comme ce second exemple, je constate qu’un très grand nombre d’exercices ou problèmes de mathématiques récréatives sont du vernis qui recouvre des connaissances trop spécifiques pour être utiles.
PS : Les termes connaissances spécifiques et abstraites ne doivent pas être prises dans le sens de la théorie de la charge cognitive : ici, connaissance abstraite = schémas au sens de la CLT ou catégories.
Les exemples ne sont qu’à titre indicatif. Ce genre de jeu mathématique, aussi simple soit-il, suscite de l’intérêt, ce qui mène à la réflexion.
La personne intéressée apprends mieux, c’est un « plus-value »… et le « plus-value » de l’enseignant n’est nécessairement pas le « plus-value » de l’élève!
Bonjour,
Chouette d’entende parler de Berloquin.Si ma m.moire ne me fait pas défaut, j’ai même un livre de lui préfacé par Gardner. Saluez-le pour moi!
@Normand Baillargeon
> Chouette d’entende parler de Berloquin.Si ma m.moire ne me fait pas défaut, j’ai même un livre de lui > préfacé par Gardner. Saluez-le pour moi!
Oui, je crois qu’il a connu Gardner qui rédigeait les préfaces des livres de Pierre traduits en anglais.
Le site de Pierre Beloquin: http://www.berloquin.com/
Claude Coulombe
Je vous trouve sévère envers Gardner et aussi peu enclin à admettre que ces jeux ne sont que des points de départ pour les enseignant.e.s qui les ajusteront selon le niveau et le curriculum.