Petites énigmes du vendredi

À chaque vendredi, je publie ici de petites énigmes logico-mathématiques ainsi que la solution des énigmes de la semaine précédente.

Merci de ne pas poster vos solutions ici, de manière à permettre à tout le monde de jouer.

Les questions demandant des éclaircissements ou des précisions sont par contre les bienvenues.

Enigmes de la semaine: la topologie amusante

La topologie est la branche des mathématiques qui s’intéresse aux propriétés des objets qui demeurent invariantes quand ils sont déformés par contraction, torsion, étirement et ainsi de suite — tout étant permis à condition de ne jamais briser ce qui est uni ou coller ce qui est séparé. On comprend pourquoi on l’appelle parfois la «géométrie de la feuille de caoutchouc».

Considérez par exemple cette tasse, qui devient un beigne. Elle le fait par transformation topologique :

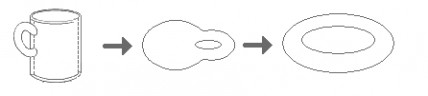
C’est pourquoi on dit qu’une topologiste est une personne qui ne fait pas la différence entre une tasse et un beigne, puisque ces deux objets sont pour elle équivalents!

On trouve en topologie de nombreux résultats étonnants ou amusants qui n’ont échappé ni aux magiciens, ni aux artistes. Voyons donc quelques trucs amusants qui illustrent cette branche des mathématiques.

Le ruban de Möbius

Prenez une bande de papier assez longue (disons 50 cm) et pas très large (disons 4 cm). Déposez-la sur la table puis, faites lui faire une demi-rotation et collez les deux extrémités avec du ruban adhésif.

Ce que vous venez de créer devrait ressembler à ce qui suit et s’appelle un Ruban de Möbius, en l’honneur de l’astronome Allemand qui l’a découvert au XIX ^ème siècle.

Plein écran

 

 

C’est un ruban très étrange. En fait, vous pouvez parier tout ce que vous voudrez avec vos amis et sans risque qu’ils ne pourront pas en colorer une face bleue et l’autre rouge. Hésitant? Vérifiez!

 

***

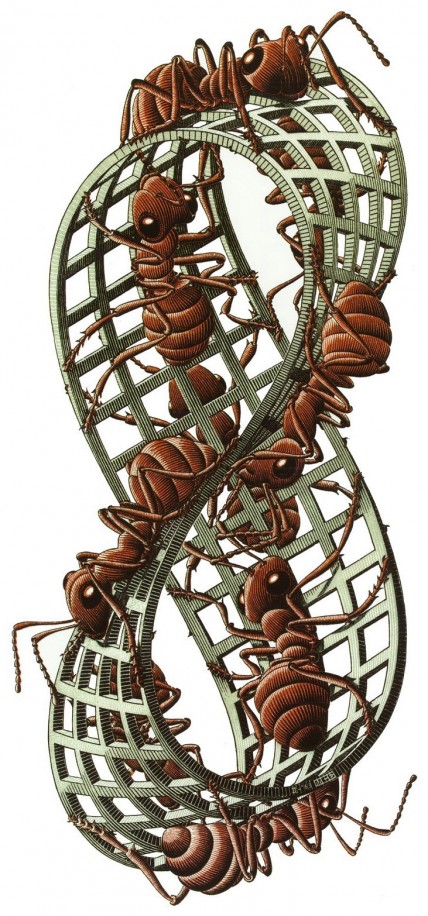
Le ruban de Möbius a en effet cette étonnante propriété de n’avoir qu’une seule face! Vous le voyez bien en la suivant du doigt : vous revenez à votre point de départ. Cette propriété a inspiré au peintre M.C. Escher (1898-1972) la célèbre image suivante :

Plein écran

***

À présent qu’on s’est fait plaisir, voici quelques jeux et énigmes.

1. Revenons au ruban de Möbius que vous avez confectionné. Supposons qu’à l’aide de ciseaux nous décidons de le couper en deux par le milieu, dans le sens de la longueur. Nous obtenons deux bandes, n’est-ce pas? Hé bien, non! Essayez-le, pour voir ce qui va arriver à votre ruban.

2. Un ruban fait avec une rotation complète n’a pas, lui, une seule surface (vérifiez-le). Que se passera-t-il si vous le coupez lui aussi en deux, toujours par le milieu et dans le sens de la longueur.

1. 13 212$

2. Il y en a … 10 992!

Vérifions. Il y a (7 enfants x 7 sacs) = 49 sacs à dos dans l’autobus. Il y a aussi 7 chattes x 49 = 343 chattes. Il y a encore 343 x 7 chatons = 2401 chatons. Ce qui nous fait : 2401 + 343 = 2744 chats. Et donc : 2744 x 4 = 10 976 pattes. À quoi il faut ajouter les (7 x 2) = 14 jambes des enfants, ce qui fait 10 990. Puis … les deux jambes du chauffeur («sept enfants sont véhiculés». On arrive ainsi à : 10 992.

3. Deux fois et demi. En allant du premier étage au troisième, vous montez de deux étages; en allant du premier étage au sixième, vous montez de cinq étages. Ce qui est cinq fois et demi plus haut.

4. On se dira peut-être qu’il grimpe donc 1 m par jour (ce qui est exact) et qu’il finira donc le parcours en 15 jours : ce qui est faux, puisque le matin du 14ème jour, il sera à deux mètres du sommet, qu’il atteindra donc cette journée-là.

5. On répond souvent spontanément 15 (i.e. 30/2).

Mais la bonne réponse est : au 29e jour. Le jour précédent, en effet, le nénuphar couvre la moitié du lac — le lendemain, il double et couvre le lac tout entier.

6. C’est la formulation du problème qui induit en erreur, de sorte qu’on ne peut attendre de l’opération 27+ 2 qu’elle donne 30. Le $27.00 représente pour les clients non le prix de la chambre, mais celui de la chambre et du bonus que s’est octroyé le chasseur. Ce montant représente les $30.00 qu’ils ont d’abord dépensés et les $3 qu’on leur a rendus. La comptabilité, qui est tout de même utile à quelque chose, rend cela très clair. Initialement, l’aubergiste a un revenu de $30.00 et les clients une dépense de $30.00. Lorsque l’aubergiste rend $5.00, il a un revenu de $30.00 — $5.00 = $25.00. Lorsque le chasseur remet $3.00 aux clients, leur dépense est maintenant de $30.00 — $3. 00 = $27. 00. LA différence entre les deux est de : $27.00 — $25.00 = $2.00, ce qui correspond au montant empoché par le chasseur.