À chaque vendredi, je publie sur ce blogue de petites énigmes logico-mathématiques, ainsi que la solution des énigmes de la semaine précédente.
Merci de ne pas poster vos solutions ici, de manière à permettre à tout le monde de jouer.
Les questions demandant des éclaircissements ou des précisions sont par contre les bienvenues.
Enigmes de la semaine:
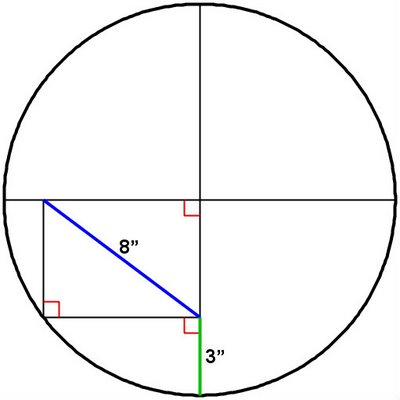
1. Pouvez-vous déterminer la longueur du rayon de ce cercle?
2. Durant la Révolte des Boxers, en Chine, en 1900, un officier étranger a vu tant de drames et est tellement épuisé qu’il s’endort pendant la messe à laquelle il assiste, un dimanche, à Pékin. Il rêve alors qu’il a été fait prisonnier des Boxers, qui l’ont jugé et condamné à mort : il en est au moment où le bourreau lève son sabre et s’apprête à l’abattre sur son cou. À cet instant très exactement, son épouse, derrière lui, constatant qu’il s’est endormi, le touche au cou avec la tranche son éventail, afin de le éveiller. Le choc psychologique est si terrible que l’officier meurt sur le champ.
Cette histoire est logiquement impossible. Dites pourquoi.
3. On fait à un prisonnier l’offre suivante : «Prononce une proposition qu’on pourra déterminer vraie ou fausse. Si elle est vraie, on te pendra. Si elle est fausse, on te fusillera». Le prisonnier a pourtant eu la vie sauve. Quelle proposition a–t-il prononcée?
Solutions aux énigmes de la semaine dernière
1. Que désigne π?
π désigne le rapport constant entre le périmètre d’un cercle (i.e. la longueur de sa circonférence) et son diamètre (qui est le double de son rayon).
En d’autres termes, et pour que ce soit bien clair : entourez un disque d’une corde : vous avez son périmètre. Passez ensuite une autre corde en son centre : vous avez son diamètre. Déposez cette corde au sol. Ouvrez ensuite la corde du périmètre, faites-en une droite et déposez là au-dessus de la corde du diamètre : elle est π fois plus grande que la corde du périmètre.
2. La ficelle autour de la Terre
Il suffira de la rallonger de … 6, 28 mètres. C’est tout et ce sera suffisant.
Pour le comprendre, revenons à notre formule permettant de calculer le périmètre d’un cercle. Ce que nous cherchons, c’est la différence entre le périmètre d’un cercle C1 et celui d’un cercle C2, dont les rayons diffèrent de 1 mètre. Appelons le rayon du premier cercle r1; celui du deuxième, r2. On sait en outre que: r2 = r 1 + 1 mètre.
Nous voulons connaître la différence des périmètres entre les deux cercles, i.e. C2 – C1. La formule du périmètre d’un cercle est 2 π r. Nous recherchons donc : 2 π r 2 – 2 π r 1.
Or :
2 π r 2 – 2 π r 1 = 2 π (r1 – r2)
Mais : r1 – r2 = 1
Donc : 2 π r 2 – 2 π r 1 = 2 π
Ce qui revient à 2 x 3, 14 = 6, 28
Il suffira donc bien d’allonger la corde de 6, 28 mètres!

Ce que je trouve amusant avec la troisième énigme, c’est qu’a priori, elle semble impossible. Après nous viennent en tête Cantor, Godël ou Turing. Ce n’est qu’en désespoir de cause, en aillant cherché en vain en m’inspirant de ces mathématiciens, que je me suis rendu compte finalement qu’il existe une infinité de propositions toutes simples !
Je m’en suis tenue à Mai 68 mais il se pourrait fort bien que je sois complètement à côté de la plaque.
Énigme n°1 résolue! Sympa le petit piège^^
Les énigmes du vendredi trône désormais en évidence sur le tableau commun de ma job. Autant répandre la bonne parole mathématique!
Merci. Ça fait plaisir, ça!
*trônent
Marie, selon les rèĝles du nouvel ortograf il n’y a pas de fautes…
Je ne suis pas tout à fait certaine de comprendre votre propos.
J’aime la première énigme. Elle est vraiment bien formulée.
Elle est chouette; je l’aime bien moi aussi.
Cher Normand, un vieil ami vivant à Rimouski vous lance un défi: résoudre l’énigme qu’il propose. La semaine dernière je lui avais fait parvenir votre énigme et il a répondu.
«Salut Jean-Serge,
La réponse à la question est assez simple, il suffit d’une petite calculatrice. La corde doit être allongée de 6,3 m environ, à la condition bien sûr qu’on considère la surface de la Terre aussi lisse que celle d’un globe terrestre, autrement dit qu’on n’ait pas à suivre les creux et les sommets des montagnes.
Pour ce qui est du nombre pi, il est défini comme le rapport entre la circonférence d’un cercle et son diamètre. J’avais déjà entendu parler de la définition « biblique » du nombre pi. C’est évidemment de la foutaise! Les textes bibliques de l’Ancien Testament ont été écrits avant que les mathématiciens définissent le nombre pi comme le rapport entre la circonférence et le diamètre d’un cercle. Il est donc stupide de dire que la Bible a une opinion sur le sujet. Les gens qui le disent font dire des choses à un texte où le sens de la précision des observateurs est aussi à questionner. L’objet était-il parfaitement rond? L’outil dont on se servait pour mesurer les coudées était-il bien étalonné? À cette époque éloignée, se contentait-on d’une précision de 10 %, comme on le fait souvent dans la vie courante? Etc, etc…
Pour ce qui est du truc mnémotechnique, j’en avais un assez semblable, fonctionnant de la même manière:
Que j’aime à faire apprendre un nombre utile aux sages.
Illustre Archimède, artiste, ingénieur,
Toi de qui Syracuse loue encore le mérite
J’ai soumis à un ami, ancien professeur de physique, un petit problème de mon cru, bien amusant:
Devant chez moi, le fleuve fait 50 km de largeur. Un baigneur (bravant l’eau froide) descend dans l’eau jusqu’à être immergé à la hauteur de ses yeux. Comme la Terre est ronde (on le pense, il me semble), même avec une vue hyper-perçante, il ne peut voir un objet sur la grève de l’autre côté du fleuve à cause de la courbure. Plantons donc un piquet de l’autre côté avec à son sommet un lumière très brillante. La question est: quelle est la hauteur minimale que ce piquet doit avoir pour que notre observateur puisse voir cette lumière?
Je connais évidemment la réponse, mais je ne te la donne pas. Tout ce que je peux te dire, c’est que la première réponse que les gens donnent est très loin de la vérité. Si tu connais NORMAND BAILLARGEON, tu peux lui soumettre mon petit problème. J’en ai quelques autres du même genre.
En passant, je me demande comment l’humanité a pu croire si longtemps que la Terre était plate, étant donné que les marins savaient depuis l’Antiquité qu’un bateau s’éloignant d’un port disparaissait peu à peu, le haut de son mât étant la dernière chose visible de lui. Je serais bien curieux de savoir quelle explication on pouvait à ce moment-là donner à ce phénomène.»
Pierre Bard, ancien prof de maths et d’informatique.
P.-S. Normand, pouvez-vous résoudre le problème proposé?
JSB
Si R= 6371 km, h la hauteur recherchée et d = 50 kms, en utilisant Pythagore ( R + h) au carré = R au carré plus D au carré, j’arrive à 196 m. J’espère ne pas dire de connerie.
Normand, je vais en parler avec mon ami qui est très friand d’énigmes et de jeux divers.
JSB
Mais si la lumière est suffisamment brillante, ne pourrait-elle pas être vue à travers l’eau du fleuve?
Bonjour, Normand!
J’attends toujours le verdict de mon ami Pierre Bard.
JSB