J’ai l’impression de vivre le jour de la marmotte. Plusieurs membres de la classe politique proposent une réforme du mode de scrutin allant vers un scrutin proportionnel et la population elle-même y est très favorable. De plus, on est en train de démarrer le processus de révision de la liste électorale.
Tout ceci serait bien intéressant, si je n’avais pas vécu cette situation à plusieurs reprises depuis 2002. La conclusion est toujours la même : on propose une variante du mode de scrutin mixte qui ne sera jamais mis en application et on ajoute des exceptions à la loi électorale pour que la carte électorale ne devienne pas trop biscornue.
Pour commencer, produire une carte électorale ne devrait pas être un exercice lourd. Avec les logiciels modernes générer une carte à peu près équitable ne prendrait que quelques minutes. Mais, pour se donner des airs démocratiques, il faut que cela coute de millions de dollars et prenne des mois. Mathématiquement, le problème est trivial, mais politiquement particulièrement complexe dans le cas du Québec.
En effet, la densité de population varie énormément sur le territoire, alors que le nombre de députés à l’Assemblée nationale n’est pas très élevé, ce qui rend problématique toute représentation territoriale effective.
Ainsi, contrairement aux prétentions des gérants d’estrade, la moyenne mondiale pour une population équivalente à celle du Québec est de l’ordre de 200 députés. Ces observations empiriques sont supportées par un modèle théorique indiquant que cela serait un optimum. La comparaison avec l’Ontario est boiteuse, car le parlement de cette province est sous-dimensionné. Un fait illustré par l’augmentation des coûts consécutifs à la réduction du nombre de députés dans un élan de populisme.
Si avoir plus de députés permettait de réduire de nombreux problèmes, il se heurte à des considérations tant politiques que pratiques. En effet, la population ne voit pas cela d’un bon œil et il n’y a guère d’espace libre restant à l’Assemblée nationale. De sorte, qu’il est peu réaliste de penser pouvoir augmenter le nombre de députés, même si cela serait la solution la plus élégante.
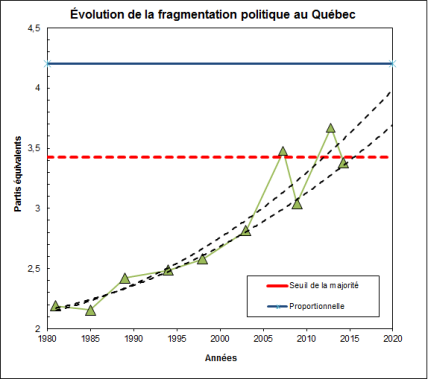
La réforme du mode de scrutin quant à elle est en train de devenir une nécessité. En effet, depuis les années 80, l’électorat québécois se fragmente de plus en plus. Cela a plusieurs conséquences néfaste : la pluralité est de moins en moins efficace pour élire le gagnant de Condorcet dans chaque circonscription, le parlement est de moins en moins représentatif et les gouvernements majoritaires sont de moins en moins possibles. Sur ce dernier point, si la tendance se maintient le présent gouvernement sera vraisemblablement le dernier gouvernement majoritaire qui ne soit pas une coalition. Il serait d’ailleurs important de faire nommer le Lieutenant-Gouverneur par l’Assemblée nationale, afin qu’il possède la légitimité nécessaire pour gérer les problèmes liés aux gouvernements de coalition.
Or, le faible nombre de députés pose un sérieux problème à toute velléité de réforme du mode de scrutin de type compensatoire qui réduirait le nombre de circonscriptions électorales. Ce type de mode de scrutin est utilisé en Allemagne où l’électeur vote à deux reprises: une fois pour l’élection locale et une fois au niveau national. On utilise le vote national pour corriger les distorsions causées par les élections locales pour que le nombre de sièges soit proportionnel en utilisant des députés supplémentaires. Typiquement, 60 % des députés sont élus au suffrage direct et 40 % sont élus de façon compensatoire.
Dans le cas du Québec, cela voudrait dire réduire à 75 le nombre de circonscriptions électorales. Les 50 députés restants serait élus à la proportionnelle de façon compensatoire ou non, selon qui fait la proposition. Il est clair que ce genre de proposition va faire face à une opposition majeure des régions qui trouvent qu’elles sont déjà représentées par des circonscriptions électorales trop étendues.
Il existe pourtant une alternative innovante qui permettrait de résoudre à la fois les problèmes de représentation territoriale effective et de représentation politique équitable. Il s’agit du scrutin majoritaire équitable : un système proportionnel avec compensation. Les électeurs votent pour un député local comme on le fait aujourd’hui. Les sièges sont par la suite distribués en proportion du nombre de votes reçus par chaque parti. La représentation territoriale est donc conservée tout en assurant une équité entre les électeurs et la proportionnalité. Ce mode de scrutin est utilisé dans un contexte de proportionnelle régionale par la ville et le canton du Zurich en Suisse en 2006, suivi des cantons de Scaffhausen et de Aargau en 2007. Il a été proposé dans de nombreux pays européens, ainsi qu’aux États-Unis.
L’originalité de la méthode est que la compensation est faite en changeant le poids de votes. L’algorithme de calcul des poids n’est pas très complexe, mais demande tout de même un certain soin. Si la mise en œuvre de l’algorithme n’est pas nécessairement à la portée de tous, une fois les poids compensatoires publiés, il est très facile de vérifier que les résultats sont exacts.
Suite aux recommandations de Michel Balinski, j’essaye de vendre ce mode de scrutin depuis 2007. Jusqu’ici, je me suis heurté à un mur. L’argument principal est que c’est trop mathématique pour le peuple québécois. J’en déduis donc que les Suisses sont nettement plus intelligents que nous.
Lecture suggérée

Le dernière déduction me semble un peu hâtive, mais merci quand même de vous intéresser à nos systèmes politiques 🙂 La Suisse étant une fédération de 26 états, il existe chez nous presque autant de systèmes électoraux, en révision permanente sous l’effet de la démocratie directe.
Or à ce jour il n’y a « que » 3 cantons qui ont adopté le système bi-proportionnel « double Pukelsheim » comme nous l’appelons ici . Un quatrième (Fribourg) est en passe de l’adopter mais il faut aussi signaler que 5 Cantons l’ont aussi rejeté, dont une fois au stade du vote populaire (Thurgovie en 2011). L’adoption de ce système au niveau fédéral a aussi été rejeté 4 fois.
Car la méthode a aussi des inconvénients, listés dans la référence ci-dessous pages 17 et 18. Notamment, il peut arriver qu’un petit parti « pique » un siège à un parti plus fort dans la circonscription voisine. Ceci peut conduire à un émiettement des partis qui a conduit Zurich et Argovie à réintroduire des quorums pour éviter l’explosion du nombre de listes. Dommage pour le « Parti des Astrophysiciens Québécois » 😉
Comme je le dis souvent, peu importe le système politique, l’important est de pouvoir le changer, et l’améliorer en permanence. Le pas entre votre système majoritaire et un système proportionnel « simple » me semble bien plus grand qu’entre un système proportionnel et un bi-proportionnel. Peut-être faut-il franchir les étapes une à une…
Référence : « Comparaison des systèmes électoraux proportionnels », Rapport de la Chancellerie Fédérale, 2011 http://bit.ly/1A9JG4N
Merci beaucoup pour cette référence très intéressante. J’avais lu sur le débat dans le canton de Genève, mais ce texte est beaucoup plus riche. Les discussions sur l’apparentement sont intéressantes, car c’est ce que j’avais en tête pour le traitement des candidats indépendants.
Il y a cependant une erreur dans l’analyse du parlement fédéral. Contrairement, ce qui est dit dans le texte, la méthode de Webster/Sainte-Laguë /Schepers ne respecte pas toujours la condition du quotient. C’est la méthode de quotient pour laquelle cela se produit le moins souvent, mais c’est tout de même une fois tous les quelques milliers d’élections. Pour la biproportionnelle, je ne suis pas certain.
Je note au passage qu’un quorum naturel de 10 %, ce qui correspond à 5 sièges par district électoral est très élevé. Dans un système proportionnel complétement développé, c’est 30 à 40 % des voies qui seront sous ce seuil.
Pour ce qui est de ma proposition, mon point est que le système proportionnel qui est le plus près du système majoritaire est le scrutin majoritaire équitable. C’est donc le plus petit pas que l’on peut faire.
Ceci dit, cette discussion est un bel exemple du mauvais usage des institutions démocratiques : la résolution d’un problème technique.
Contrairement à ce que vous semblez croire, la méthode de Webster (dite, en France, méthode de Sainte-Lagüe) est légèrement biaisée en faveur des grands partis. Il existe évidemment une unique méthode non biaisée ; elle se fonde, non pas sur l’idée que la répartition des sièges doit minimiser les écarts par rapport à une répartition rigoureusement proportionnelle, mais sur l’idée qu’elle doit minimiser les écarts de pouvoir de vote entre les citoyens apportant leurs suffrages aux différents partis en présence.
Par ailleurs, tout système qui divise le corps électoral en organisant une multitude de consultations locales peut entraîner un véritable déni de démocratie. C’est le cas pour le suffrage universel indirect qui, aux États-Unis, a déjà permis à plusieurs reprises l’élection d’un président ayant obtenu moins de voix que son adversaire. C’est aussi le cas du scrutin uninominal qui, en France, permet régulièrement à la majorité parlementaire d’adopter des lois contre la volonté des députés élus par la majorité de la population, députés qui, par la grâce de ce système électoral, ne représentent qu’une minorité de l’Assemblée nationale.
Je me permets de renvoyez à mon site Web pour plus de détails.
La méthode de Webster/Sainte-Lagüe n’est pas biaisée. C’est un résultat classique.
Je crois comprendre que vous utilisez l’interprétation du pouvoir des votes de Robert Penrose. Elle a court dans le milieu, mais elle est erronée.
Une répartition strictement proportionnelle attribuerait à chaque circonscription ou à chaque parti un nombre de siège rigoureusement proportionnel à sa population ou au nombre de suffrages recueillis, nombre qui serait donc toujours décimal. Dans ce cas, le rapport de la part effective de sièges à la quote-part théorique serait toujours égal à 1. En pratique, on est bien obligé d’arrondir les quotes-parts de manière à attribuer des nombres entiers de députés. Que peut-on alors exiger d’une méthode de répartition ? Deux choses nous semble-t-il :
1) que la répartition soit le plus proche possible de la répartition proportionnelle idéale, c’est-à-dire qu’elle minimise la somme des écarts |P/QP – 1| ;
2) qu’elle ne favorise ni les petites ni les grandes circonscriptions, c’est-à-dire que la moyenne des rapports P/QP soit égal à 1 a priori, aussi bien, par exemple, pour l’infinité des circonscriptions dont la quote-part est comprise entre 1 et 2 que pour l’infinité de celles dont la quote-part est comprise entre 21 et 22.
Qu’en est-il de la méthode de Webster ? Elle satisfait très généralement à la première condition, quoiqu’il soit facile d’exhiber des contre-exemples. Si l’on veut qu’elle minimise la somme des écarts |P/QP-1| dans toute répartition particulière, il convient de lui apporter une modification ad hoc. Par contre, modifiée ou non, elle ne vérifie pas la seconde condition, le rapport moyen P/QP étant plus faible pour les petites circonscriptions que pour les grandes. Ceci est mathématiquement incontestable et, après cela, on peut toujours la déclarer « non-biaisée ».
Existe-t-il au moins une méthode qui satisfasse pleinement aux deux conditions ? La réponse est oui, si l’on accepte de se baser, non pas sur le rapport P/QP, mais sur la racine carrée de ce rapport. Or, la racine carrée de ce rapport n’est rien d’autre que la forme standardisée du pouvoir brut de Banzhaff. Le pouvoir brut de Banzhaff (P) est une probabilité liée à la probabilité de satisfaction de l’électeur par la formule :
S = 1/2 + P/2
Le pouvoir standardisé de Banzhaff mesure la même probabilité avec une unité différente, mais fixe pour toute situation de répartition donnée (ce qui n’est pas le cas du pouvoir normalisé de Banzhaff).
La question de biais est traitée dans Balinski et Young Fair Representation. À vue de nez, votre méthode ressemble à la méthode de Hill, qui est utilisée pour le Congrès américain.
Pour revenir à ce que je disais plus tôt, votre interprétation de l’indice de Banzhaff-Coleman est la même que celle de Robert Penrose. Or, cette dernière n’est vrai que dans un cas limite, auquel cas le pouvoir des électeur est 1/sqrt(n). Dans un général d’échantillonnage de l’électorat, le pouvoir moyen revient de l’électeur redevient en 1/n.
L’objection que je soulève concerne toute répartition proportionnelle quelle qu’elle soit. Elle n’est pas le moins du monde conditionnée par la notion préalable de pouvoir de vote. Elle aboutit à une méthode qui dégénère a priori, et seulement a priori, en une méthode de diviseur utilisant, pour diviseur, la moyenne arithmétique entre le diviseur arithmétique de Webster et le diviseur géométrique de Hill. Le fait que l’on retombe alors nécessairement sur le pouvoir brut de Banzhaf n’est qu’une simple conséquence des deux conditions souhaitées (cf. supra).
Mais je ne souhaite pas insister davantage si ce que j’avance va à l’encontre des résultats « démontrés » par les spécialistes de la question.
La méthode de Webster possède aussi d’autres propriétés de consistances qui la rendent supérieure aux autres méthodes. En effet, on peut définir la proportionnalité de différentes façons, ce qui donne autant de mode de scrutin non-biaisés que de définition du biais. Sauf que si l’on ajoute des critères de consistance, seul Webster passe le test.
Pour ce qui est de l’indice de pouvoir de Benzhaff, l’erreur très généralement commise est de ne tenir compte que du cas limite p=q=0,5, ce qui donne une distribution du pouvoir en 1 sur racine de n. Par contre, si on tiens compte de toutes les valeurs de p et q, le pouvoir va en 1/n. C’est Warren D. Smith qui en a fait la démonstration. La dernière fois que j’ai communiqué avec lui, il n’avait pas réussit à publier son résultat.
Dernière tentative pour essayer au moins de faire comprendre mon objection. Il est incontestable que, dans une circonscription élisant un nombre de députés P, la méthode de Webster assimile le pouvoir du citoyen à P/Popuation ou, ce qui revient au même moyennant un coefficient de proportionnalité égal au quotient électoral, à la valeur standardisée P/Quote-Part. Il est encore incontestable qu’elle minimise les écarts de pouvoir ainsi défini, mais uniquement a priori. Pour atteindre cet objectif dans tous les cas en pratique, il faut utiliser une méthode plus générale qui ne se réduit à celle de Webster qu’a priori. Mais cette première remarque n’a que peu d’importance.
Si l’on utilise la méthode de Webster, on l’utilise dans tous les cas, y compris lorsque p=q et que, vous l’indiquez, le pouvoir est inversement proportionnel à la racine carrée de la population. Or c’est, me semble-t-il, le cas général en démocratie. Dans leur histoire, les États-Unis ont élu presque exactement le même nombre de présidents républicains ou démocrates et en France, lors des législatives, on n’a jamais vu ni la droite ni la gauche recueillir 60% des suffrages, loin s’en faut. Faut-il en conclure que la méthode de Webster ne serait légitime que dans un régime totalitaire ? Mais cette remarque polémique (dont je m’excuse humblement) elle non plus, n’est pas fondamentale.
Sans entrer dans les détails mathématiques, de chaque coté de p=q=0,5 la valeur du pouvoir diminue exponentiellement. La largeur de la courbe est de l’ordre de racine de n. Ce qui est l’équivalent de l’incertitude dans un sondage. On a donc racine de n au carré (n).
On peut aussi imaginer le cas d’une élection dans 10 circonscriptions électorales pour une assemblée de 10 candidats. Si on part du principe que le pouvoir serait proportionnel à la racine de n, on aurait plus de pouvoir dans cette configuration que dans un scrutin direct, ce qui est absurde (1/10 au lieu de 1/100).
Warren D. Smith en fait la démonstration formelle au début de son article #56:
http://rangevoting.org/WarrenSmithPages/homepage/works.html
Si l’on s’accorde au moins sur le fait que, en effet, une méthode de répartition équitable doit limiter autant que faire se peut les écarts de pouvoir entre les circonscriptions, il convient de partir d’une loi statistique très générale, valable qu’elle que soit la valeur relative de p et de de q (et il est donc inutile de revenir sur cette aspect des choses), disant que les écarts à la moyenne théorique (laquelle vaut 1 pour le rapport P/QP) sont inversement proportionnels à la racine carrée du nombre d’épreuves (électoralement, à la racine carrée du nombre de suffrages exprimés). Et j’avoue que j’ai un léger doute quant au fait que qui que ce soit serait parvenu à démontrer le contraire.
Oubliez ma dernière intervention (celle de 11h06) ; ma pensée est allée plus vite que mes doigts sur le clavier et il en résulte un propos absurde.
1) L’ensemble des circonscriptions dont la quote-part est comprise entre 1 et 2 doivent obtenir, globalement, le même nombre de députés que si elles étaient réunies en une circonscription unique. 2) une circonscription doit avoir un nombre de députés proportionnel à sa population. 3) le pouvoir standardisé d’une circonscription ayant droit à P députés se mesure par le rapport P/Quote-Part.
Cette unique affirmation, présentée de trois manières différentes, implique la méthode de Webster ou une méthode qui lui soit équivalente a priori. Si l’on s’avise alors de calculer le pouvoir moyen standardisé dans chaque intervalle de quotes-parts on trouve environ 0,981 pour l’intervalle [1,2] mais 1,000 pour l’intervalle [11,12] : l’égalité absolue entre les citoyens n’est pas réalisée. Est-elle possible ? Oui, mais à la seule condition de partir de l’affirmation : la racine carrée du nombre de députés doit être proportionnelle à la racine carrée de la population. Et c’est évidemment valable si l’on décide du nombre d’hôpitaux à construire dans chaque circonscription. Bref, la valeur relative de p et de q est totalement hors de propos.
Ces deux affirmations sont mutuellement exclusives:
-Une circonscription doit avoir un nombre de députés proportionnel à sa population.
-La racine carrée du nombre de députés doit être proportionnelle à la racine carrée de la population.
La deuxième affirmation se justifie par l’interprétation de Penrose sur le pouvoir des votes. Je ne comprends pas votre référence aux hôpitaux. Est-ce que vous faites référence à une contrainte spatiale?
Les deux affirmations sont rigoureusement équivalentes pour une répartition en nombres fractionnaires mais aboutissent à des répartitions en nombre entiers très légèrement différentes. S’agissant des hôpitaux, je veux dire que l’important n’est pas que chaque habitant, où qu’il habite, ait droit à la même parcelle d’hôpital (point de vue de Webster) mais qu’il ait la même probabilité de satisfaction (= de pouvoir se faire soigner près de chez lui). De même pour le vote : chacun aura la même parcelle de député (Webster) ou la même probabilité de satisfaction. Sauf que Webster n’accorde même pas la même parcelle moyenne à tous les intervalles de quotes-parts !